Re: [escepticos] Exprimiendo la coincidencia

["Rafael Budría" <rbudria@...>]

Mig escribió:
> 
> Rafael Budría wrote:


> [Mig] Hola Rafael, gracias por la ayuda, realmente habia notado que la
> superficie de la esfera es igual a la de un cilindro con igual radio,
> pero no consigo ver facilmente si al cortar en rebanadas iguales la
> esfera y el cilindro, la superficie rebanada alrededor se mantiene
> constante en la esfera (en el cilindro es logico que si).

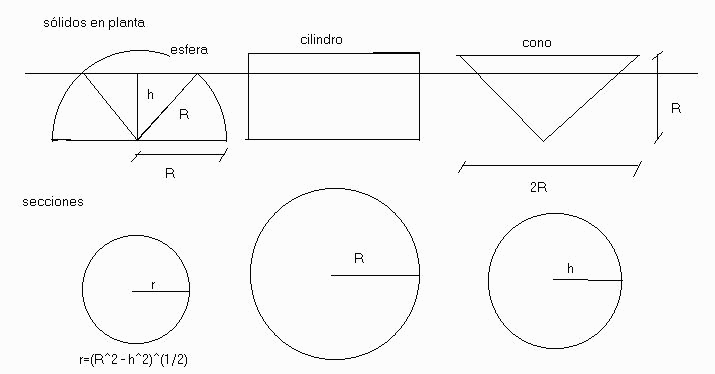
 Nada, te mando un dibujito. No soy una mago de diseño pero puede pasar.

 La demostración es la siguiente. La sección de las tres figuras se
efectúa a una altura h<R (con R siendo tanto el radio de la
(semi)esfera, las alturas del cono y el cilindro y radio de las bases
del cilindro y el cono). Las sección del cilindro vale pi*R^2 (es
constante), la del cono pi*h^2 (el cono mide de alto tanto como de radio
de la base, así pues el radio de la sección tiene el mismo valor que la
distancia del plano de sección al vértice. Por semejanza de triángulos).
La de la esfera es algo más complicada pero sale por Pitágoras aplicado
al triángulo formado por los radios que van a parar del centro de la
(semi)esfera (usted ya me entiende) a la intersección del plano de
sección con la esfera y cuya longitud es R (según dibujo). Así pues, el
cuadrado del radio de la sección (circular como todas ellas) de la
esfera vale R^2-h^2 Es fácil de comprobar que la sección del cilindro es
la suma de las secciones del cono y la esfera a cualquier altura h.

 La demostración concluye así. Si consideramos las secciones como
pequeñas rebanadas del sólido se cumple que el volumen de cada rebanada
del cilindro es igual al de las rebanadas del cono y la esfera juntos
(al ser las rebanadas muy finas no importa que estas no sean exactamente
cilindros sino pequeños troncos de cono puesto que la diferencia será
menor cuanto más finas sean las rebanadas y será nula en el límite de
infinitas rebanadas infinìtamente finas). Al cumplirse esta relación
para cada rebanada y puesto que las rebanadas suman los volúmenes de los
tres cuerpos que estábamos considerando tenemos

Volumen_semi_esfera=Volumen_cilindro - Volumen_cono. O sea 

Volumen_cono = (1/3) del área de la base [pi*R^2] por la altura [R en
nuestro caso]

Volumen_cilindro=área de la base [pi*R^2] por la altura [R en nuestro
caso]

Volumen_semi_esfera = pi*R^3 - (1/3)*pi*R^3 =(2/3)*pi*R^3

Volumen_esfera=2*Volumen_semi_esfera=(4/3)*pi*R^3

 Saludos.


 Sobre la
> formula que mencione arriba no se si es la misma que pueden haber usado
> los antiguos, yo solo hice una analogia con los pedazos pizza, solo que
> ahora los pedazos son tridimensionales, con la punta en el centro de la
> esfera y la base en su superficie. Bueno, si un pobre corralero lo ve
> por que no el gran Arqui?